Cadence, or the number of steps runners take per minute, is a data point that's calculated on many GPS watches, but no one knows quite what to do with it. For decades, we've been told that. A byte is a sequence of 8 bits The 'leftmost' bit in a byte is the biggest. So, the binary sequence 00001001 is the decimal number 9. 00001001 = (2 3 + 2 0 = 8 + 1 = 9). Bits are numbered from right-to-left. Bit 0 is the rightmost and the smallest; bit 7 is leftmost and largest. We can use these basic agreements as a building block to exchange. NUTRIENT CALCULATOR Select your VEG and FLOWER lengths. 5.7 - 5.9 for Hydro; 5.7 - 6.2 for Coco Coir; 6.2 - 6.8 for Soil.DO NOT add Magic Green to your.
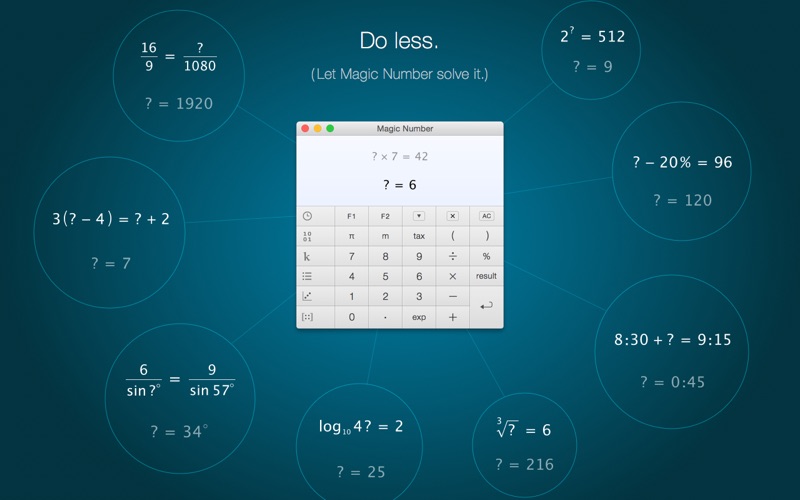
- Magic Number 2 7 8 – A Better Calculator Percentage
- Magic Number 2 7 8 – A Better Calculator Present Value
| Magic Square |
Contents of this Page
|
| To the Main Page 'Mathematische Basteleien' |
| ..............8....1....6......................... ..............3....5....7......................... ..............4....9....2......................... | You can assemble the numbers 1 to 9 in a square, so that the sum of the rows, the columns, and the diagonals is 15. If you take the numbers 1 to 9, you have the standard square. |
| .............8+c....1+c....6+c.............. .............3+c....5+c....7+c.............. .............4+c....9+c....2+c.............. | A magic square remains magic, if you change each numbers by a constant c. You add c on the left. You can also subtract, multiply or divide. |
The Magic 3x3 Square top
You have 1+2+3+4+5+6+7+8+9=45. In a magic square you have to add 3 numbers again and again. Therefore the average sum of three numbers is 45:3=15. The number 15 is called the magic number of the 3x3 square.
You can also achieve 15, if you add the middle number 5 three times.
Magic Number 2 7 8 – A Better Calculator Percentage
| 15=1+5+9 15=1+6+8 | 15=2+4+9 15=2+5+8 | 15=2+6+7 15=3+4+8 | 15=3+5+7 15=4+5+6 |
Therefore you have to place number 5 in the middle of the magic 3x3 square. The remaining odd numbers have to be in the middles of a side and the even numbers at the corners.
Under these circumstances there are eight possibilities building a square: All the eight squares change into each other, if you reflect them at the axes of symmetry. You count symmetric squares only once. Therefore there is only one magic 3x3 square.
The Magic 4x4 Squaretop
The magic number is (1+2+...+15+16):4 = 34.
The computer found 86 reductions of 34 to a sum of four summands with the numbers 1 to 16.
| 34=01+02+15+16 34=01+03+14+16 34=01+04+13+16 34=01+04+14+15 34=01+05+12+16 34=01+05+13+15 34=01+06+11+16 34=01+06+12+15 34=01+06+13+14 34=01+07+10+16 34=01+07+11+15 34=01+07+12+14 34=01+08+09+16 34=01+08+10+15 34=01+08+11+14 34=01+08+12+13 34=01+09+10+14 34=01+09+11+13 | 34=01+10+11+12 34=02+03+13+16 34=02+03+14+15 34=02+04+12+16 34=02+04+13+15 34=02+05+11+16 34=02+05+12+15 34=02+05+13+14 34=02+06+10+16 34=02+06+11+15 34=02+06+12+14 34=02+07+09+16 34=02+07+10+15 34=02+07+11+14 34=02+07+12+13 34=02+08+09+15 34=02+08+10+14 34=02+08+11+13 | 34=02+09+10+13 34=02+09+11+12 34=03+04+11+16 34=03+04+12+15 34=03+04+13+14 34=03+05+10+16 34=03+05+11+15 34=03+05+12+14 34=03+06+09+16 34=03+06+10+15 34=03+06+11+14 34=03+06+12+13 34=03+07+08+16 34=03+07+09+15 34=03+07+10+14 34=03+07+11+13 34=03+08+09+14 34=03+08+10+13 | 34=03+08+11+12 34=03+09+10+12 34=04+05+09+16 34=04+05+10+15 34=04+05+11+14 34=04+05+12+13 34=04+06+08+16 34=04+06+09+15 34=04+06+10+14 34=04+06+11+13 34=04+07+08+15 34=04+07+09+14 34=04+07+10+13 34=04+07+11+12 34=04+08+09+13 34=04+08+10+12 34=04+09+10+11 34=05+06+07+16 | 34=05+06+08+15 34=05+06+09+14 34=05+06+10+13 34=05+06+11+12 34=05+07+08+14 34=05+07+09+13 34=05+07+10+12 34=05+08+09+12 34=05+08+10+11 34=06+07+08+13 34=06+07+09+12 34=06+07+10+11 34=06+08+09+11 34=07+08+09+10 . . . . |
| Summand: Number: | 01 19 | 02 20 | 03 21 | 04 22 | 05 22 | 06 23 | 07 23 | 08 22 | 09 22 | 10 23 | 11 23 | 12 22 | 13 22 | 14 21 | 15 20 | 16 19 |
Fact: There are 880 magic squares, counting the symmetric ones only once.
This is one of 880 possible squares:
| ............12....06....15.....01............ ............13....03....10.....08............ ............02....16....05.....11............ ............07....09....04.....14............ | This square is special. The number 34 is not only the sum of the numbers in the rows, the columns, and both diagonals, but also in every 2x2 square. |
The magic number is (1+2+...+24+25) : 5 = 65.
Reductions of the magic number 65.
| 65 = 01+02+13+24+25 65 = 01+02+14+23+25 65 = ... 65 = ... | 65 = ... 65 = ... 65 = 10+12+13+14+16 65 = 11+12+13+14+15 | The computer found 1394 reductions of the number 65. |
Making of a magic 5x5-square:
You go through the numbers 1 to 25. There are two rules for constructing a magic square 'top right' and 'if the place is occupied, go one down'.
| ......................................... | Number 1 is placed in the centre of the first row. Number 2 follows top right. But then you leave the 5x5 square.Therefore you must imagine the square is a cylinder. The cylinder has the vertical square sides of the square as circumference. The horizontal sides touch each other and close the curved surface of the cylinder. So there is a field top right for number 2. If you unroll the cylinder, number 2 has gone to the last row one place to the right. |
| ...... | Number 4 would lie outside the 5x5 square. So again you imagine the square would become a cylinder, this time with vertical axis. You can find a place for number 4. If you unroll the cylinder, you find the number in the third row on the far left. |
You use the second rule for number 6. If the field top right is occupied, you put the number one row down in the same column.
You go further on with 7, 8, and so on. - You use the same rule for number 16 as for number 6.
You can transfer this way of formation to all magic squares with odd numbers of the sides ;-).
There are also rules for magic squares with an even side length. They are more complicated however.
The Magic nxn Squareetop
The existence of magic squares nxn is proved for all numbers n>2. But there is no general rule.
The magic number is (1 + 2 + 3 + ... + n²) : n =0.5 * (n²+1) * n.
Magic squares: 3x3 4x4 5x5 6x6 7x7 8x8 9x9 10x10
Magic numbers: 15 34 65 111 175 260 369 505
Curiosities top
| ... | Once again: A square is magic, if the numbers have the same sum in the rows, the columns and the diagonals. |
| ...... | A square is semi-magic, if the numbers have the same sum only in the rows and the columns. |
| ...... | A square is pandiagonal, if it is magic and if not only the numbers of the main diagonals, but also the broken diagonals have the same sum. |
| ... | This magic square is pandiagonal. |
| ...... | You find the complementary square, if you replace each number n by 17-n. |
Magic Number 2 7 8 – A Better Calculator Present Value
The square is self-complemetary, because the new one is symmetric to the old one. See red axis.| ...... | A square is associative, if it is magic and if pairs of numbers lying symmetrically to the centre have the same sum. The sum is 26=5²+1 =n²+1. |
| ... | The 3x3 magic square Lo Shu is associative. |
| ... | A magic square with prime numbers |
| ... | A 'semi'-magic square of square numbers All sums going through the centre have the same value. Source: http://www.mathpages.com/home/kmath417.htm |
>panmagic squares
>magic squares formed by smaller magic squares
>bordered magic squares (Book 2).
There is an explanation for all the different magic squares: They can be found by computers. A new property means a new query inside the program.
Simple Variants top
Magic Squares on the Internet top
English
Craig Knecht (Magic Square Models)| Water Retention Patterns | ...... | Imagine, the squares are the top of square prisms with the height given by the numbers. If you pour water in this solid, it stays in the centre upto the height 17. Then it flows off. The amount of water is (17-3)+(17-7)+(17-13)+(17-1)+(17-4)+(17-5)=69. There are nice problems: Biggest amount of water? Seperate ponds? Island? |
Eric W. Weisstein (MathWorld)
Magic Square, Panmagic Square, Associative Magic Square, Lo Shu
Harvey D. Heinz
Magic Squares, Magic Stars & Other Patterns
Holger Danielsson
Magic Squares
Ivars Peterson's MathTrek
More than Magic Squares
Mark S. Farrar
Magic Squares
MathPages
Solving Magic Squares
Robin Moseley
Magic Flexagon (.pdf-File)
Wikipedia
Magic square, Most-perfect magic square, Water retention on mathematical surfaces, Associative magic square
German
Feng-Shui-Homepage
Das magische Quadrat Lo-Shu
Gerd Müller
Magisches Quadrat interaktiv
Hans-Peter Gramatke
Magische Quadrate
Holger Danielsson
Magische Quadrate
Jan Haase
Das Hexeneinmaleins aus Goethes 'Faust' (Lösung)
Jan Theofel und Martin Trautmann
Magische Quadrate und Würfel

Under these circumstances there are eight possibilities building a square: All the eight squares change into each other, if you reflect them at the axes of symmetry. You count symmetric squares only once. Therefore there is only one magic 3x3 square.
The Magic 4x4 Squaretop
The magic number is (1+2+...+15+16):4 = 34.
The computer found 86 reductions of 34 to a sum of four summands with the numbers 1 to 16.
| 34=01+02+15+16 34=01+03+14+16 34=01+04+13+16 34=01+04+14+15 34=01+05+12+16 34=01+05+13+15 34=01+06+11+16 34=01+06+12+15 34=01+06+13+14 34=01+07+10+16 34=01+07+11+15 34=01+07+12+14 34=01+08+09+16 34=01+08+10+15 34=01+08+11+14 34=01+08+12+13 34=01+09+10+14 34=01+09+11+13 | 34=01+10+11+12 34=02+03+13+16 34=02+03+14+15 34=02+04+12+16 34=02+04+13+15 34=02+05+11+16 34=02+05+12+15 34=02+05+13+14 34=02+06+10+16 34=02+06+11+15 34=02+06+12+14 34=02+07+09+16 34=02+07+10+15 34=02+07+11+14 34=02+07+12+13 34=02+08+09+15 34=02+08+10+14 34=02+08+11+13 | 34=02+09+10+13 34=02+09+11+12 34=03+04+11+16 34=03+04+12+15 34=03+04+13+14 34=03+05+10+16 34=03+05+11+15 34=03+05+12+14 34=03+06+09+16 34=03+06+10+15 34=03+06+11+14 34=03+06+12+13 34=03+07+08+16 34=03+07+09+15 34=03+07+10+14 34=03+07+11+13 34=03+08+09+14 34=03+08+10+13 | 34=03+08+11+12 34=03+09+10+12 34=04+05+09+16 34=04+05+10+15 34=04+05+11+14 34=04+05+12+13 34=04+06+08+16 34=04+06+09+15 34=04+06+10+14 34=04+06+11+13 34=04+07+08+15 34=04+07+09+14 34=04+07+10+13 34=04+07+11+12 34=04+08+09+13 34=04+08+10+12 34=04+09+10+11 34=05+06+07+16 | 34=05+06+08+15 34=05+06+09+14 34=05+06+10+13 34=05+06+11+12 34=05+07+08+14 34=05+07+09+13 34=05+07+10+12 34=05+08+09+12 34=05+08+10+11 34=06+07+08+13 34=06+07+09+12 34=06+07+10+11 34=06+08+09+11 34=07+08+09+10 . . . . |
| Summand: Number: | 01 19 | 02 20 | 03 21 | 04 22 | 05 22 | 06 23 | 07 23 | 08 22 | 09 22 | 10 23 | 11 23 | 12 22 | 13 22 | 14 21 | 15 20 | 16 19 |
Fact: There are 880 magic squares, counting the symmetric ones only once.
This is one of 880 possible squares:
| ............12....06....15.....01............ ............13....03....10.....08............ ............02....16....05.....11............ ............07....09....04.....14............ | This square is special. The number 34 is not only the sum of the numbers in the rows, the columns, and both diagonals, but also in every 2x2 square. |
The magic number is (1+2+...+24+25) : 5 = 65.
Reductions of the magic number 65.
| 65 = 01+02+13+24+25 65 = 01+02+14+23+25 65 = ... 65 = ... | 65 = ... 65 = ... 65 = 10+12+13+14+16 65 = 11+12+13+14+15 | The computer found 1394 reductions of the number 65. |
Making of a magic 5x5-square:
You go through the numbers 1 to 25. There are two rules for constructing a magic square 'top right' and 'if the place is occupied, go one down'.
| ......................................... | Number 1 is placed in the centre of the first row. Number 2 follows top right. But then you leave the 5x5 square.Therefore you must imagine the square is a cylinder. The cylinder has the vertical square sides of the square as circumference. The horizontal sides touch each other and close the curved surface of the cylinder. So there is a field top right for number 2. If you unroll the cylinder, number 2 has gone to the last row one place to the right. |
| ...... | Number 4 would lie outside the 5x5 square. So again you imagine the square would become a cylinder, this time with vertical axis. You can find a place for number 4. If you unroll the cylinder, you find the number in the third row on the far left. |
You use the second rule for number 6. If the field top right is occupied, you put the number one row down in the same column.
You go further on with 7, 8, and so on. - You use the same rule for number 16 as for number 6.
You can transfer this way of formation to all magic squares with odd numbers of the sides ;-).
There are also rules for magic squares with an even side length. They are more complicated however.
The Magic nxn Squareetop
The existence of magic squares nxn is proved for all numbers n>2. But there is no general rule.
The magic number is (1 + 2 + 3 + ... + n²) : n =0.5 * (n²+1) * n.
Magic squares: 3x3 4x4 5x5 6x6 7x7 8x8 9x9 10x10
Magic numbers: 15 34 65 111 175 260 369 505
Curiosities top
| ... | Once again: A square is magic, if the numbers have the same sum in the rows, the columns and the diagonals. |
| ...... | A square is semi-magic, if the numbers have the same sum only in the rows and the columns. |
| ...... | A square is pandiagonal, if it is magic and if not only the numbers of the main diagonals, but also the broken diagonals have the same sum. |
| ... | This magic square is pandiagonal. |
| ...... | You find the complementary square, if you replace each number n by 17-n. |
Magic Number 2 7 8 – A Better Calculator Present Value
The square is self-complemetary, because the new one is symmetric to the old one. See red axis.| ...... | A square is associative, if it is magic and if pairs of numbers lying symmetrically to the centre have the same sum. The sum is 26=5²+1 =n²+1. |
| ... | The 3x3 magic square Lo Shu is associative. |
| ... | A magic square with prime numbers |
| ... | A 'semi'-magic square of square numbers All sums going through the centre have the same value. Source: http://www.mathpages.com/home/kmath417.htm |
>panmagic squares
>magic squares formed by smaller magic squares
>bordered magic squares (Book 2).
There is an explanation for all the different magic squares: They can be found by computers. A new property means a new query inside the program.
Simple Variants top
Magic Squares on the Internet top
English
Craig Knecht (Magic Square Models)| Water Retention Patterns | ...... | Imagine, the squares are the top of square prisms with the height given by the numbers. If you pour water in this solid, it stays in the centre upto the height 17. Then it flows off. The amount of water is (17-3)+(17-7)+(17-13)+(17-1)+(17-4)+(17-5)=69. There are nice problems: Biggest amount of water? Seperate ponds? Island? |
Eric W. Weisstein (MathWorld)
Magic Square, Panmagic Square, Associative Magic Square, Lo Shu
Harvey D. Heinz
Magic Squares, Magic Stars & Other Patterns
Holger Danielsson
Magic Squares
Ivars Peterson's MathTrek
More than Magic Squares
Mark S. Farrar
Magic Squares
MathPages
Solving Magic Squares
Robin Moseley
Magic Flexagon (.pdf-File)
Wikipedia
Magic square, Most-perfect magic square, Water retention on mathematical surfaces, Associative magic square
German
Feng-Shui-Homepage
Das magische Quadrat Lo-Shu
Gerd Müller
Magisches Quadrat interaktiv
Hans-Peter Gramatke
Magische Quadrate
Holger Danielsson
Magische Quadrate
Jan Haase
Das Hexeneinmaleins aus Goethes 'Faust' (Lösung)
Jan Theofel und Martin Trautmann
Magische Quadrate und Würfel
Maria Koth
Magische Quadrate (.pdf.-Datei)
Paul Heimbach
Magische Quadrate
recordholders.org
Das größte Magische Quadrat der Welt
Udo Hebisch (Mathematisches Café)
Magische Quadrate
Wikipedia
Magisches Quadrat, Vollkommen perfektes magisches Quadrat
Referencestop
(1) Bild der Wissenschaften, Heft 8/1966, Heft 6/1968, Heft 10/1976
(2) Pieter van Delft /Jack Botermans: Denkspiele der Welt, München 1980 (1998 neu aufgelegt)
(3) Maximilian Miller, Gelöste und ungelöste mathematische Probleme, Leipzig 1982
This page is also available in German with more details.
URL of my Homepage:
http://www.mathematische-basteleien.de/
© 2000 Jürgen Köller
top